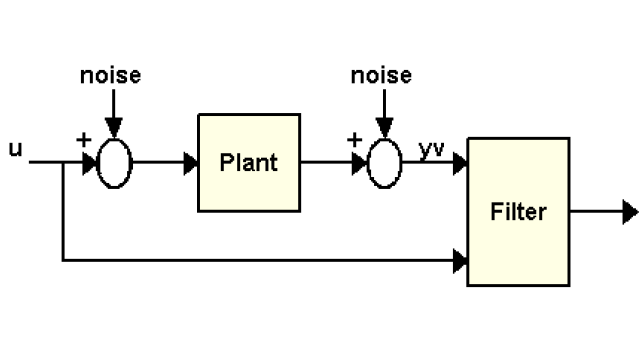
If you've heard of the Kalman filter before but haven't had a chance to understand what it is, how it helps us solve state estimation problems, or how to implement one yourself, then this is the journey for you. It is broken up into several sections:
- Prerequisites - the information you might need before starting this journey
- Introduce the basic concepts - an overview of the filter with minimal mathematics
- Watch others use it - Check out the Kalman filter in action on other people's projects
- Try it yourself - A few different ways to implement and test the filter on your own
- Fundamentals - A more mathematically rigorous approach to the filter
- Other variations - Looking at the EKF, UKF, and expanding into the particle filter
- Other material - Things to check out if you're interested in exploring some more
Prerequisites: It might be helpful to start with a really big picture look at sensor fusion so that you have a better understanding of why it's important to learn the Kalman filter. If you're already motivated to learn and have a basic understanding of sensor fusion then you can absolutely skip this video without getting confused later on.
Understanding Sensor Fusion and Tracking, Part 1: What Is Sensor Fusion?
This video provides an overview of what sensor fusion is and how it helps in the design of autonomous systems. It also covers a few scenarios that illustrate the various ways that sensor...
See MorePrerequisites: If you haven't had much experience with state space representation, you may want to brush up on the basics with this resource. Again, you can skip this if you just want to get to the Kalman filter without having to watch a bunch of videos first!
State Space, Part 1: Introduction to State-Space Equations
Let’s introduce the state-space equations, the model representation of choice for modern control. This video is the first in a series on MIMO control and will provide some intuition around...
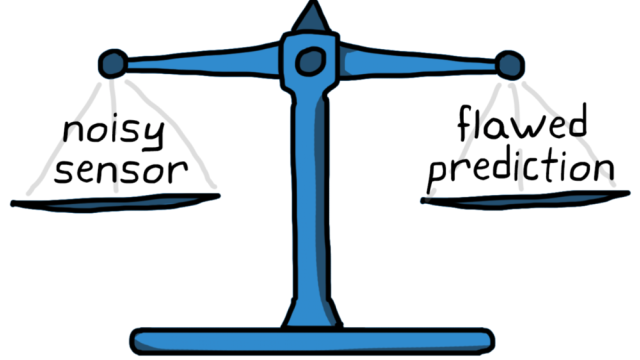
See MoreIntroduce the basic concept: Let's begin with a gentle introduction to the Kalman filter. This article doesn't provide a rigorous explanation, but I think it'll help you form a basic understanding of what the Kalman filter is and how it can estimate state given a set of noisy sensors and a flawed model of the system.
The Kalman Filter
This article introduces the Kalman filter at a high level and tries to provide some insight into how the filter is able to estimate state by combining measurements and models.
This is an...
See MoreIntroduce the basic concept: I find that sometimes you need to read the same information from two different people in order for it to really stick in your mind. So, if you're still struggling with understanding how multiplying all of these different matrices can produce an optimal state estimate, check out this article by Tim Babb. If you feel that you have a pretty good handle on it from the last resource then you can skip this, however, I recommend you check it out at least for the amazing visuals!
How a Kalman Filter Works in Pictures
This article builds up some intuition about the Kalman filter using pictures before diving into the mathematics. A beginner will come away with an understanding of what the Kalman filter is...
See MoreWatch others use it - Joe Barnard builds some incredible thrust vector controlled model rockets and he uses a Kalman filter to estimate the kinematic state of the rockets (position, velocity, orientation). In this video, he's describing the components of the flight computer. The whole thing is worth a watch but check out 13:50-14:35 to understand how the Kalman filter contributes to the overall design.
The AVA Flight Computer
This video describes the board design, hardware architecture, and software components of the All Vehicle Avionics (AVA) flight computer that was designed by Joe Barnard of BPS Space. This...
See MoreWatch others use it - If you watched the above video, check out this one where Joe shows the results of flying Sprint (with the Kalman filter). At about 5:50 he describes some of the telemetry he receives from the rocket and starting at about 7:50 he describes the output of the Kalman filter.
Sprint - Test Flight 8 and Data Review
This video is part of a series that details the design, build, and test of Sprint - a thrust vector controlled model rocket by Joe Barnard of BPS Space.
See MoreTry it yourself: Probably the best way to have all of this sink in is to play around with the algorithm yourself. If you have access to MATLAB and Simulink, this model allows you to tweak the parameters of a Kalman filter and watch how it impacts the estimation.
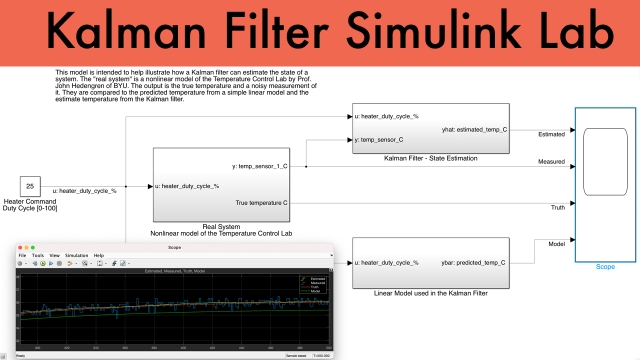
Kalman Filter Simulink 2022A example
This model is intended to help illustrate how a Kalman filter can estimate the state of a system. The "real system" is a nonlinear model of the Temperature Control Lab by Prof. John...
See MoreTry it yourself: This is another example that is good if you have access to MATLAB and the Control System Toolbox. This example walks through designing your own filter.
Kalman Filter Design
This example shows how to perform Kalman filtering. Both a steady state filter and a time varying filter are designed and simulated.
See MoreTry it yourself: If you're looking to implement an extended Kalman filter (EKF) on an Arduino or other microcontroller, check out TinyEKF.
TinyEKF: Lightweight C/C++ Extended Kalman Filter with Python for prototypin...
TinyEKF is a simple C/C++ implementation of the Extended Kalman Filter that is general enough to use on different projects. In order to make it practical for running on Arduino, STM32, and...
See MoreFundamentals: Now that we have the basic idea of the Kalman filter, I think we're more prepared to dive deeper into the mathematics.
An Introduction to the Kalman Filter
The purpose of this paper is to provide a practical introduction to the discrete Kalman filter. This introduction includes a description and some discussion of the basic discrete Kalman...
See MoreOther variations of estimation filters: With an understanding of how the basic Kalman filter can be used to estimate state, we can start to look at other forms of estimation filters. This article does a great job building up intuition around the extended Kalman filter, the sigma-point filter, and the particle filter. Don't pass on this resource - at least read the introduction where he talks about how we use more information than just direct measurements to estimate state. Worth a read!
How Kalman Filters Work, Part 1
This article looks at four popular estimation filter architectures: particle filter, sigma point filter, extended Kalman filter, and the Kalman filter. It discusses how all four of these...
See MoreOther variations of estimation filters: Check out this video if you want to see how some state estimation problems are inherantly non-Gaussian and, therefore, not suitable for a Kalman filter.
Autonomous Navigation, Part 2: Understanding the Particle Filter
This video presents a high-level understanding of the particle filter and shows how it can be used in Monte Carlo localization to determine the pose of a mobile robot inside a building. We...
See MoreOther material: If you want to go back to where this all started you can read R.E. Kalman's original paper.
A New Approach to Linear Filtering and Prediction Problems
A transcription of R.E. Kalman's seminal paper. Transcribed by John Lukesh, 20 January 2002
The classical filtering and prediction problem is re-examined using the Bode- Shannon...
See More