A mathematical model is a description of a system using mathematical concepts and language. The process of developing a mathematical model is termed mathematical modeling. Mathematical models are used in the natural sciences (such as physics, biology, earth science, chemistry) and engineering disciplines (such as computer science, electrical engineering), as well as in non-physical systems such as the social sciences (such as economics, psychology, sociology, political science). Mathematical models are also used in music, linguistics and philosophy (for example, intensively in analytic philosophy).
Topic
Modeling (Dynamics)
This topic includes the following resources and journeys:
Filters
Type
Experience
Scope
6 items
What Are Dynamic Models? Chapter 1 from Dynamic Models in Biology
Beginner
Book
Theory
Throughout this book we use a wide-ranging set of case studies to illustrate different aspects of models and modeling. In this introductory chapter we describe and give examples of different...
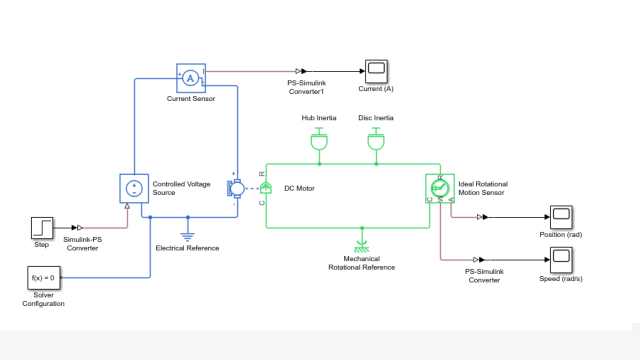
See More
Using Simscape™ to Model a Quanser QUBE-Servo 2 with Friction
15 min
Intermediate
Article / Blog
Theory
Modelling a DC servomotor is one of the common examples used in control system textbooks and courses. Given that so many systems use DC motors, e.g. robot manipulator arms, it’s an important...
See More
Perspectives on Control-Relevant Identification Through the Use of Interacti...
Intermediate
Peer Reviewed Paper
Theory
This paper presents a control-relevant identification methodology through an intuitive interactive tool called "Interactive Tool for Control Relevant Identification (ITCRI)". ITCRI...
See More
Manuscript about ITISE: an Interactive Software Tool for System Identificati...
Intermediate
Peer Reviewed Paper
Theory
The paper describes the conceptual basis, main features and functionality of an interactive software tool developed in support of system identification education and discovery.
This...
See More
Averaging Methods in Nonlinear Dynamical Systems
Intermediate
Book
Theory
Perturbation theory and in particular normal form theory has shown strong growth during the last decades. So it is not surprising that the authors have presented an extensive revision of the...
See More
Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields...
Beginner
Book
Theory
From the reviews: "This book is concerned with the application of methods from dynamical systems and bifurcation theories to the study of nonlinear oscillations. Chapter 1 provides a review...
See More