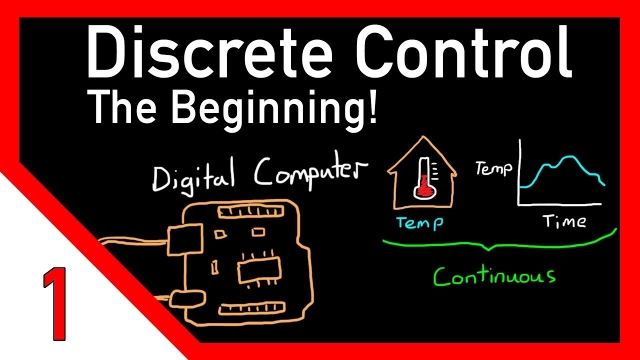
Digital control is a branch of control theory that uses digital computers to act as system controllers. Depending on the requirements, a digital control system can take the form of a microcontroller to an ASIC to a standard desktop computer. Since a digital computer is a discrete system, the Laplace transform is replaced with the Z-transform. Since a digital computer has finite precision (See quantization), extra care is needed to ensure the error in coefficients, analog-to-digital conversion, digital-to-analog conversion, etc. are not producing undesired or unplanned effects.
Since the creation of the first digital computer in the early 1940s the price of digital computers has dropped considerably, which has made them key pieces to control systems because they are easy to configure and reconfigure through software, can scale to the limits of the memory or storage space without extra cost, parameters of the program can change with time (See adaptive control) and digital computers are much less prone to environmental conditions than capacitors, inductors, etc.







![Controllability and the Discrete-Time Impulse Response [Control Bootcamp]](/sites/default/files/styles/search_resulkts/public/2020-12/maxresdefault_302.jpg?itok=xjXmM9_U)