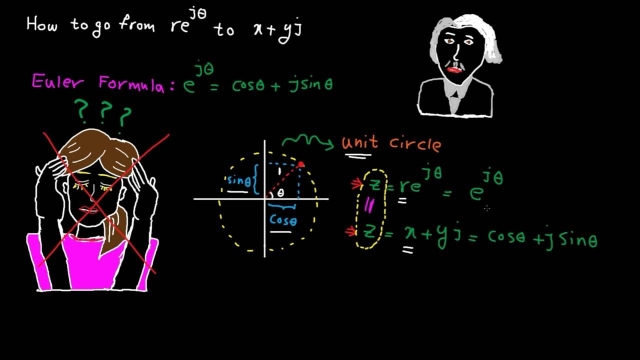Transfer Functions: Introduction and Implementation

In this video we introduce transfer functions and show how they can be derived from a set of linear, ordinary differential equations. We also examine how to...

See More

Lecture 21: Introduction to Frequency Response

This video introduces Frequency Response and Frequency Domain Specifications. Thanks to Ames Bielenberg whose animation has been made use of, in this video. See More

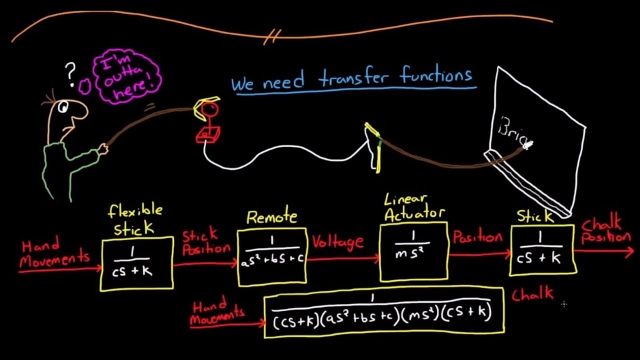
Control Systems Lectures - Transfer Functions

This lecture describes transfer functions and how they are used to simplify modeling of dynamic systems.

See More

Computing Euler Angles: The Euler Kinematical Equations and Poisson’s Kinema...

In this video we discuss how the time rate of change of the Euler angles are related to the angular velocity vector of the vehicle. This allows us to design an algorithm to consume...

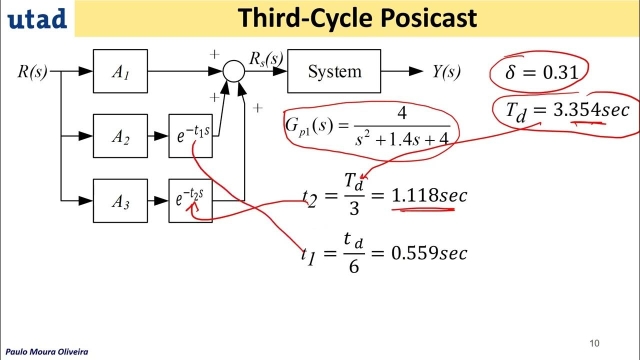
See More

Posicast Control 6 - ( In English)

This video presents the transition from half-cycle to other cycles ( third-cycle, fourth-cycle,..)

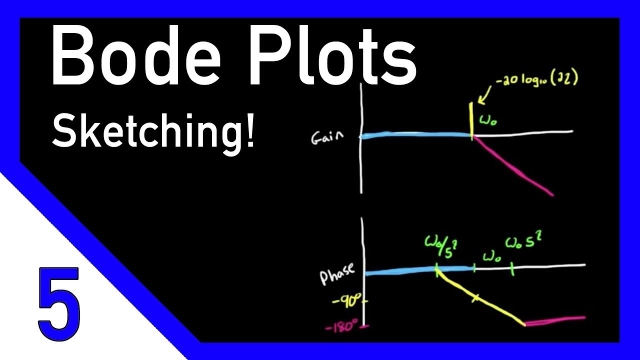
See More

Lecture 23: Bode plots

Discusses Bode plots and Bode plots for some common factors in a transfer function See More

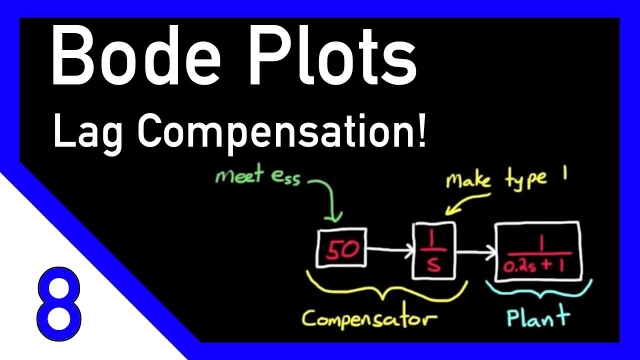
Designing a Lag Compensator with Bode Plot

This video walks through a phase lag compensator example using the Bode Plot method.

See More

Derivation of the 1D Wave Equation

In this video, we derive the 1D wave equation. This partial differential equation (PDE) applies to scenarios such as the vibrations of a continuous string. ...

See More

SVD and Alignment: A Cautionary Tale

This video describes the importance of data alignment when performing the singular value decomposition (SVD). Translations and rotations both present challenges for the SVD.

See More

crash course on complex numbers

In this video, we quickly review “Complex Numbers”. The following materials are covered:1- Cartesian and polar representation of complex numbers2- how to con...

See More

Understanding Sensor Fusion and Tracking, Part 2: Fusing a Mag, Accel, and G...

This video describes how we can use a magnetometer, accelerometer, and a gyro to estimate an object’s orientation. The goal is to show how these sensors contribute to the solution, and to...

See More

Bode Plots by Hand: Complex Poles or Zeros

This is a continuation of the Control Systems Lectures. This video describes the benefit of being able to approximate a Bode plot by hand and explains what a Bode plot looks like for a...

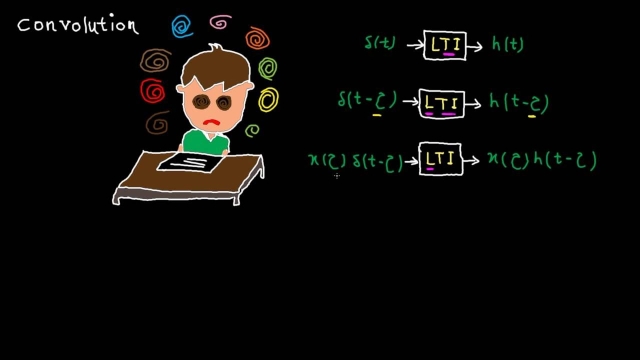
See More

Time domain - tutorial 8: LTI systems, impulse response & convolution

In this video, the following materials are covered:1) the beauty of linear & time invariant (LTI) systems2) why the impulse response of an LTI system is so i...

See More

IMC PID Design of a Second Order Process

IMC PID Design of a Second Order Process

See More

Stanford CS234: Reinforcement Learning | Winter 2019 | Lecture 16 - Monte Ca...

Professor Emma Brunskill
Assistant Professor, Computer Science
Stanford AI for Human Impact Lab
Stanford Artificial Intelligence Lab
Statistical Machine Learning Group

See More

Second Order Dynamics

A crash course overview on second order dynamics in the frequency domain, what the key parameters are, and why they matter.

See More

Data-Driven Control: Error Bounds for Balanced Truncation

In this lecture, we derive error bounds for the balanced truncation.

See More

Smart Projectile State Estimation Using Evidence Theory

This journal article provides a very good practical understanding of Dempster-Shafer theory using sensor fusion and state estimation as the backdrop.

See More

Peter Ponders PID - Yet Another Linear Quadratic Control Video but...

This videos covers topics not found or hard to find in control books or other videos.This video converts tracking position, velocity and acceleration for a m... See More

Drone Simulation and Control, Part 3: How to Build the Flight Code

This video describes how to create quadcopter flight software from the control architecture developed in the last video. It covers how to process the raw sensor readings and use them with...

See More

Trimming a Model of a Dynamic System Using Numerical Optimization

In this video we show how to find a trim point of a dynamic system using numerical optimization techniques. We generate a cost function that corresponds to ...

See More

Using a Homogeneous Transformation Matrix to Combine Rotation and Translatio...

In this video we discuss how to properly deal with coordinate frames that are both rotated and translated from one another. We develop a homogeneous transfo...

See More

Peter Ponders PID - System Identification Basics

Transfer functions don't come with the machine you are trying to control. Transfer functions must be estimated using system identification techniques. With... See More

Parseval's Theorem

Parseval's theorem is an important result in Fourier analysis that can be used to put guarantees on the accuracy of signal approximation in the Fourier domain.

See More

Routh-Hurwitz Criterion, Beyond Stability

This video explains of few uses of the Routh-Hurwitz Criterion that go beyond simply determining how many poles exist in the right half plane. I cover how to determine gain margin and how...

See More