Humans, Robots, and Non-Prehensile Manipulation

This is a fun video that was inspired by a presentation I saw at the 2015 International Conference on Robotics and Automation (ICRA). I wanted to see if humans could duplicate the...

See More

SVD: Eigenfaces 1 [Matlab]

This video describes how the singular value decomposition (SVD) can be used to efficiently represent human faces, in the so-called "eigenfaces" (Matlab code, part 1).

See More

Transfer Function to State Space

In this video we show how to transform a transfer function to an equivalent state space representation. We will derive various transformations such as contr...

See More

Data-Driven Control: Balancing Transformation

In this lecture, we derive the balancing coordinate transformation that makes the controllability and observability Gramians equal and diagonal. This is the critical step in balanced model...

See More

SVD: Eigenfaces 3 [Python]

This video describes how the singular value decomposition (SVD) can be used to efficiently represent human faces, in the so-called "eigenfaces" (Python code, part 3).

See More

Introduction to Ordinary Differential Equations

In this video we introduce the concept of ordinary differential equations (ODEs). We give examples of how these appear in science and engineering as well as...

See More

Understanding Sensor Fusion and Tracking, Part 2: Fusing a Mag, Accel, and G...

This video describes how we can use a magnetometer, accelerometer, and a gyro to estimate an object’s orientation. The goal is to show how these sensors contribute to the solution, and to...

See More

Least Squares Regression and the SVD

This video describes how the SVD can be used to solve linear systems of equations. In particular, it is possible to solve nonsquare systems (overdetermined or underdetermined) via least...

See More

Gaussian/Normal Distributions

In this video we discuss the Gaussian (AKA Normal) probability distribution function. We show how it relates to the error function (erf) and discuss how to ...

See More

Machine Learning Control: Genetic Algorithms

This lecture provides an overview of genetic algorithms, which can be used to tune the parameters of a control law.

See More

The Routh-Hurwitz Stability Criterion

In this video we explore the Routh Hurwitz Stability Criterion and investigate how it can be applied to control systems engineering. The Routh Hurwitz Stabi...

See More

Essence of Linear Algebra: Understand the Geomterical Beauty in Linear Algeb...

Linear Algebra is a very important and fundamental topic needed in almost every field of STEM. While the linear part of it is easy to understand and perform operations on, the geometric...

See More

Fourier Series [Matlab]

This video will describe how to compute the Fourier Series in Matlab.

See More

Understanding Model Predictive Control, Part 3: MPC Design Parameters

To successfully control a system using an MPC controller, you need to carefully select its design parameters. This video provides recommendations for choosing the controller sample time...

See More

Using Root Locus to Meet Performance Requirements

In this video we investigate how to use the root locus technique to design a controller that meets certain performance specifications.Topics and timestamps:(...

See More

The Fourier Transform and Derivatives

This video describes how the Fourier Transform can be used to accurately and efficiently compute derivatives, with implications for the numerical solution of differential equations.

See More

Frequency domain – tutorial 13: sampling (theory of everything in signal pro...

In this video, we learn about sampling which enables us to travel from analog to digital world. The following materials are covered:1) why traveling to the ...

See More

A Nonlinear, 6 DOF Dynamic Model of an Aircraft: the Research Civil Aircraft...

In this video we develop a dynamic model of an aircraft by describing forces and moments generated by aerodynamic, propulsion, and gravity that act on the aircraft. This video outlines the...

See More

Peter Ponders PID, Natural Frequency vs Frequency of Acceleration

This video is intended for servo hydraulic system designers and those that program hydraulic servo systems but it does show how several of the techniques sho...

See More

Control Systems with MATLAB - Time Domain Analysis

Time domain analysis has been carried out using MATLAB in this video. Second order systems have been discussed in detail. How to obtain different time domain... See More

Time domain - tutorial 9: convolution examples

In this video, we use a systematic approach to solve lots of examples on convolution. By the end of this lecture, you should be able to find convolution betw...

See More

Setting Up Your Radio Connection - dRehmFlight VTOL

This video will show you how to set up your radio to work with dRehmFlight VTOL. The code supports PWM, PPM, and SBUS type receivers, allowing you to connect and use 6 channels within the...

See More

Peter Ponders PID - Observers/Estimators

Observers can provide betters estimates of state variables when there is noise and low resolution feed back. This is often necessary to compute the higher d... See More

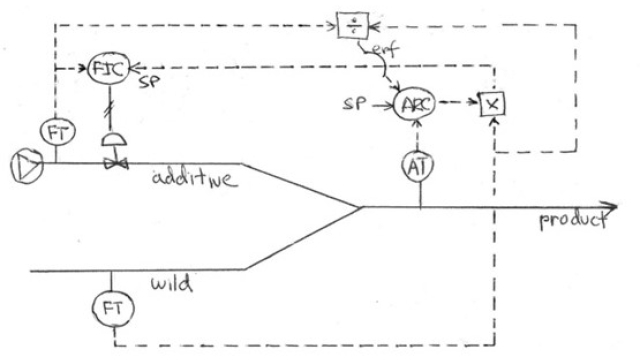
Ratio Control and Scaled Signal Calculations

When and how to use ratio, and how to implement within standard scaled signals

See More

Tutorial on Root Locus

Few numerical problems using Root locus has been explained in this video See More