In control system theory, the Routh–Hurwitz stability criterion is a mathematical test that is a necessary and sufficient condition for the stability of a linear time-invariant (LTI) control system. The Routh test is an efficient recursive algorithm that English mathematician Edward John Routh proposed in 1876 to determine whether all the roots of the characteristic polynomial of a linear system have negative real parts. German mathematician Adolf Hurwitz independently proposed in 1895 to arrange the coefficients of the polynomial into a square matrix, called the Hurwitz matrix, and showed that the polynomial is stable if and only if the sequence of determinants of its principal submatrices are all positive. The two procedures are equivalent, with the Routh test providing a more efficient way to compute the Hurwitz determinants than computing them directly. A polynomial satisfying the Routh–Hurwitz criterion is called a Hurwitz polynomial.
Topic
Routh-Hurwitz Criterion
This topic includes the following resources and journeys:
Type
Experience
Scope
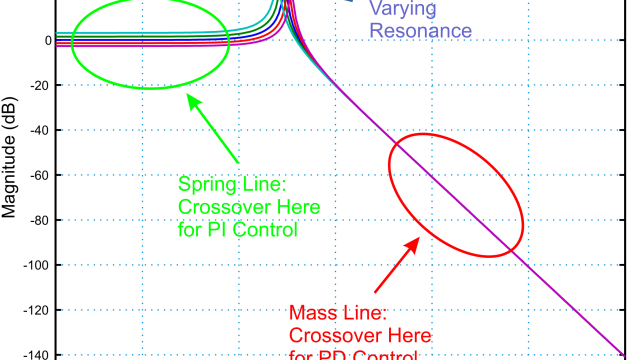
What's a Control System and Why Should I Care? A whirlwind tour through the ...
This paper aims to provide some introduction, a cheat sheet, and some context for college level STEM students about to take that first controls class. In some cases, it provides context...
See MoreRouth-Hurwitz Criterion, Beyond Stability
This video explains of few uses of the Routh-Hurwitz Criterion that go beyond simply determining how many poles exist in the right half plane. I cover how to determine gain margin and how...
See MoreRouth-Hurwitz Criterion, An Introduction
This video gives an introduction into the Routh-Hurwitz Criterion and the Routh Array. I also present a little background information in order to emphasize why the method was developed and...
See MoreThe Routh-Hurwitz Stability Criterion
In this video we explore the Routh Hurwitz Stability Criterion and investigate how it can be applied to control systems engineering. The Routh Hurwitz Stabi...
See MoreLecture 14: Routh Hurwitz Criterion
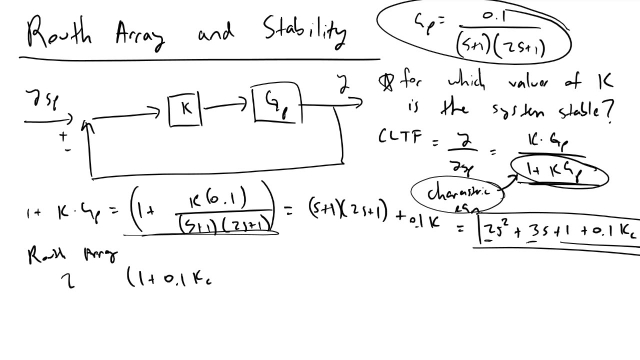
Routh Array and Stability
I show how we can find the range of allowed controller gains for a system that will allow us to maintain stability using a Routh Array.
See MoreTUTORIAL on Stability and Routh Hurwitz criterion
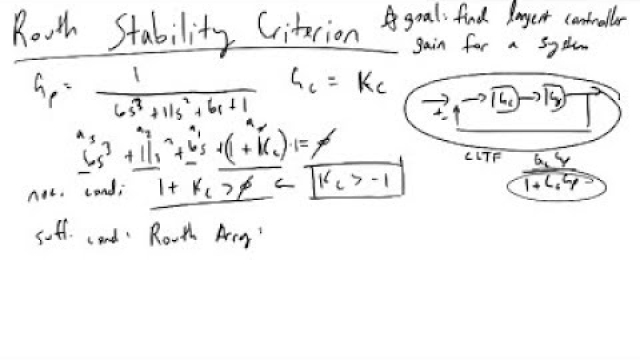
Routh Stability Criterion Intro and Example
I introduce and walk through an example problem of how we can use the Routh Stability Criterion to rigorously determine the necessary and sufficient conditio...
See MoreLecture 13: Stability and Routh Hurwitz criterion
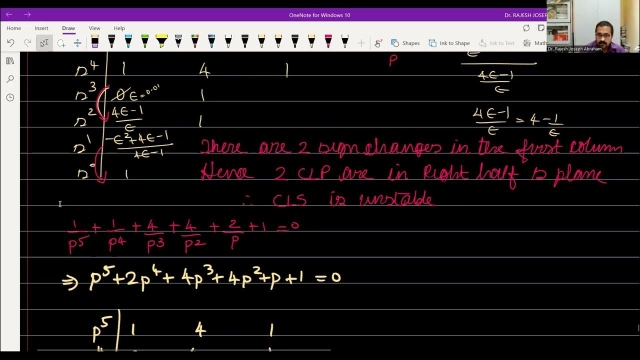
Routh-Hurwitz Criterion, Special Cases
This video presents two special cases that you can encounter when filling out the Routh Array. The first case is when there is a zero in a row with at least one non-zero element following...
See More