In mathematics, linearization is finding the linear approximation to a function at a given point. The linear approximation of a function is the first-order Taylor expansion around the point of interest. In the study of dynamical systems, linearization is a method for assessing the local stability of an equilibrium point of a system of nonlinear differential equations or discrete dynamical systems. This method is used in fields such as engineering, physics, economics, and ecology.
Topic
Linearization
This topic includes the following resources and journeys:
Filters
Type
Experience
Scope
7 items
Trimming and Linearization, Part 1: What is Linearization?
14 min
Beginner
Video
Theory
Why go through the trouble of linearizing a model? To paraphrase Richard Feynman, it’s because we know how to solve linear systems. With a linear model we can more easily design a controller...
See More
Trimming and Linearization, Part 2: The Practical Side of Linearization
11 min
Beginner
Video
Theory
With a general understanding of linearization, you might run into a few snags when trying to linearize realistic nonlinear models. These snags can be avoided if you have a more practical...
See More![Linearizing Around a Fixed Point [Control Bootcamp]](/sites/default/files/styles/search_resulkts/public/2020-12/maxresdefault_442.jpg?itok=nt2vg0vl "Linearizing Around a Fixed Point [Control Bootcamp]")
Linearizing Around a Fixed Point [Control Bootcamp]
30 min
Beginner
Video
Theory
This lecture describes how to obtain linear system of equations for a nonlinear system by linearizing about a fixed point. This is worked out for the simple pendulum "by-hand" and in...
See More
Control Design Onramp with Simulink
60 min
Beginner
Software
Demonstration
Learn the basics of feedback control design in Simulink®. Adjust the gains of a PID controller to change the dynamics of a physical system and get the closed-loop system behavior that you...
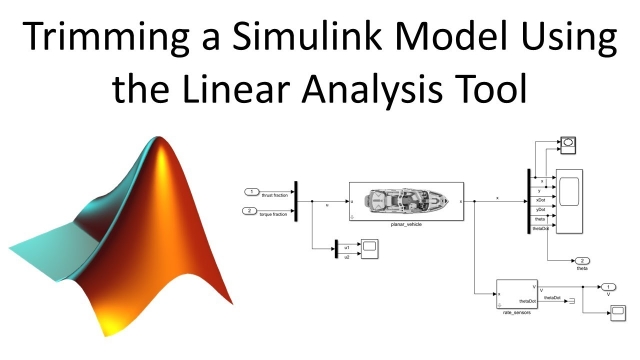
See More
Trimming a Simulink Model Using the Linear Analysis Tool
68 min
Beginner
Video
Application
In this video we show how to use the Linear Analysis Tool to trim a non-linear Simulink model. This is also known as finding an operating point or an equili...
See More
Linearizing a Simulink Model Using the Linear Analysis Tool and ‘linmod’
55 min
Beginner
Video
Application
In this video we show how to linearize a non-linear Simulink model using numerical techniques. This approach is extremely powerful as it allows automatic ge...
See More
Numerically Linearizing a Dynamic System
104 min
Beginner
Video
Theory
In this video we show how to linearize a dynamic system using numerical techniques. In other words, the linearization process does not require an analytical...
See More