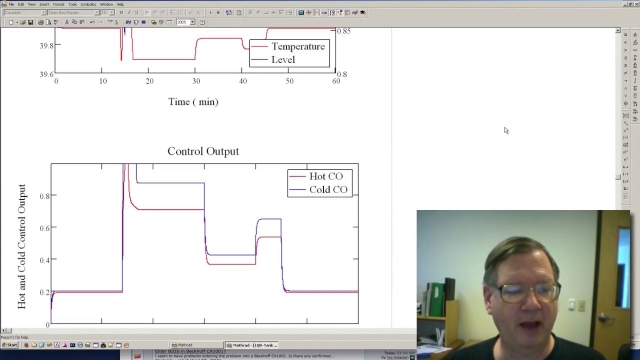
In control theory, the linear–quadratic–Gaussian (LQG) control problem is one of the most fundamental optimal control problems. It concerns linear systems driven by additive white Gaussian noise. The problem is to determine an output feedback law that is optimal in the sense of minimizing the expected value of a quadratic cost criterion. Output measurements are assumed to be corrupted by Gaussian noise and the initial state, likewise, is assumed to be a Gaussian random vector.
Under these assumptions an optimal control scheme within the class of linear control laws can be derived by a completion-of-squares argument.[1] This control law which is known as the LQG controller, is unique and it is simply a combination of a Kalman filter (a linear–quadratic state estimator (LQE)) together with a linear–quadratic regulator (LQR). The separation principle states that the state estimator and the state feedback can be designed independently. LQG control applies to both linear time-invariant systems as well as linear time-varying systems, and constitutes a linear dynamic feedback control law that is easily computed and implemented: the LQG controller itself is a dynamic system like the system it controls. Both systems have the same state dimension.









![Linear Quadratic Regulator (LQR) Control for the Inverted Pendulum on a Cart [Control Bootcamp] Linear Quadratic Regulator (LQR) Control for the Inverted Pendulum on a Cart [Control Bootcamp]](/sites/default/files/styles/search_resulkts/public/2020-12/maxresdefault_431.jpg?itok=vs89WnA2)