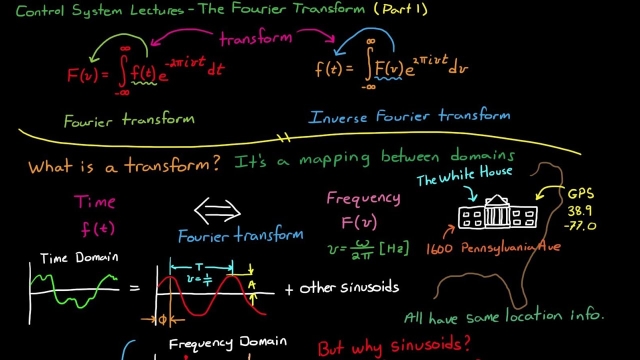
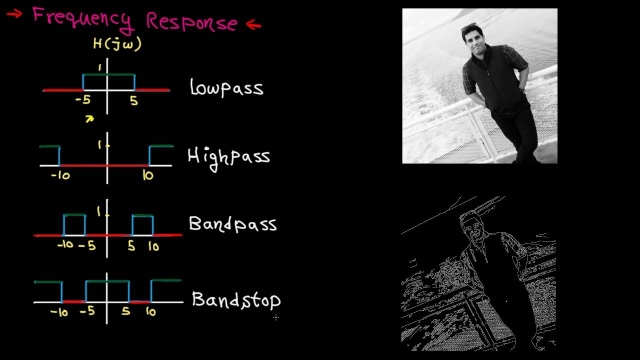
In mathematics, Fourier analysis is the study of the way general functions may be represented or approximated by sums of simpler trigonometric functions. Fourier analysis grew from the study of Fourier series, and is named after Joseph Fourier, who showed that representing a function as a sum of trigonometric functions greatly simplifies the study of heat transfer.
Today, the subject of Fourier analysis encompasses a vast spectrum of mathematics. In the sciences and engineering, the process of decomposing a function into oscillatory components is often called Fourier analysis, while the operation of rebuilding the function from these pieces is known as Fourier synthesis. For example, determining what component frequencies are present in a musical note would involve computing the Fourier transform of a sampled musical note. One could then re-synthesize the same sound by including the frequency components as revealed in the Fourier analysis. In mathematics, the term Fourier analysis often refers to the study of both operations.
The decomposition process itself is called a Fourier transformation. Its output, the Fourier transform, is often given a more specific name, which depends on the domain and other properties of the function being transformed. Moreover, the original concept of Fourier analysis has been extended over time to apply to more and more abstract and general situations, and the general field is often known as harmonic analysis. Each transform used for analysis has a corresponding inverse transform that can be used for synthesis.





![Fourier Series and Gibbs Phenomena [Matlab] Fourier Series and Gibbs Phenomena [Matlab]](/sites/default/files/styles/search_resulkts/public/2020-12/maxresdefault_363.jpg?itok=YEl5oqig)





![Fourier Series [Python] Fourier Series [Python]](/sites/default/files/styles/search_resulkts/public/2020-12/maxresdefault_362.jpg?itok=VuzjvIsu)



![Fourier Series [Matlab] Fourier Series [Matlab]](/sites/default/files/styles/search_resulkts/public/2020-12/maxresdefault_361.jpg?itok=HDuxGf-8)