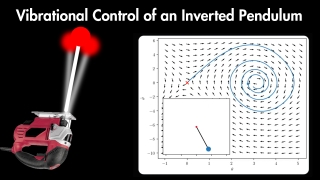
Abstract. This paper investigates averaging theory and oscillatory control for a large class of mechanical systems. A link between averaging and controllability theory is presented by relating the key concepts of averaged potential and symmetric product. Both analysis and synthesis results are presented within a coordinate-free framework based on the theory of affine connections.
The analysis focuses on characterizing the behavior of mechanical systems forced by high ampli- tude high frequency inputs. The averaged system is shown to be an affine connection system subject to an appropriate forcing term. If the input codistribution is integrable, the subclass of systems with Hamiltonian equal to “kinetic plus potential energy” is closed under the operation of averaging. This result precisely characterizes when the notion of averaged potential arises and how it is related to the symmetric product of control vector fields. Finally, a notion of vibrational stabilization for mechanical systems is introduced and provide sufficient conditions are provided in the form of linear matrix equality and inequality tests.