Here is the MATLAB Tech Talk video on nonlinear system identification. If you've already seen the video and are just looking for the references that I used to make it then keep on scrolling!

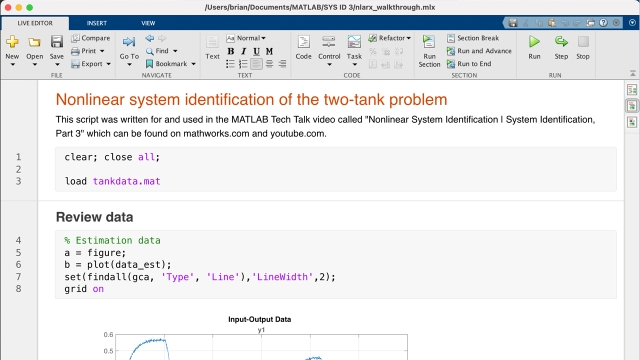
I've posted the simple MATLAB script to Github that I used in the video. I think a good way to use it would be to modify some of the parameters of the different system identification functions and see how it impacts the result. Check it out!

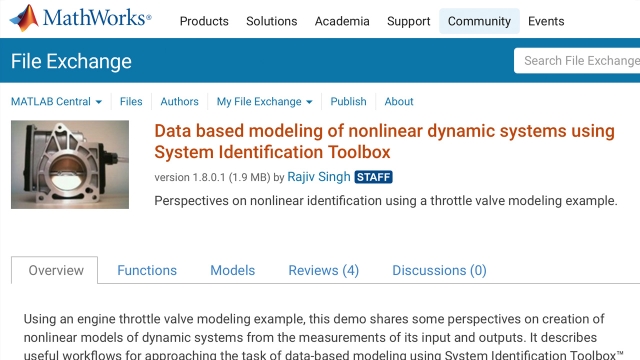
This MATLAB script is amazing and was the inspiration for the way I decided to build up the nonlinear ARX model from a linear ARX model, to an offset term, to nonlinear regressors, and finally to a nonlinear output function. There is way more in this script than what I covered and I recommend you check it out if you'd like to see multiples ways to do system identification on a single dataset. 

This page does a good job of laying out the overview of nonlinear model identification. Plus, it could be used as a launch point for exploring the dozens of other pages that Mathworks has created on all things nonlinear system identification related. 

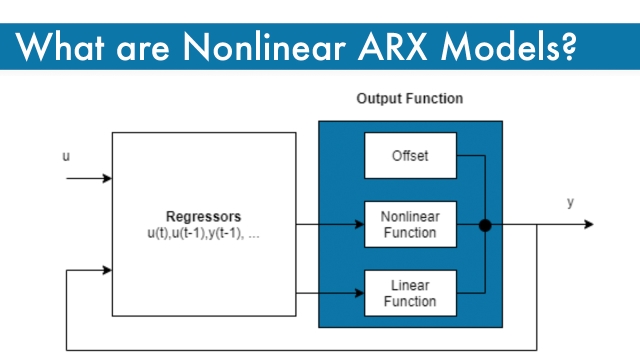
If you want to learn a bit more about nonlinear ARX models then check out this page. It goes through the math that I showed in the video (but not in like 15 seconds like I did!)

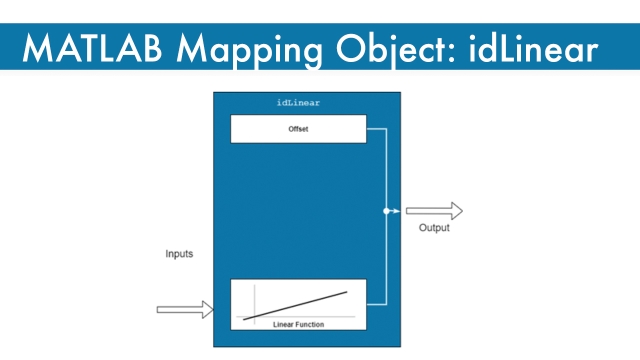
I put this here since I mentioned it in the video but if you're not specifically using idLinear in your project you can safely skip this resource for now.

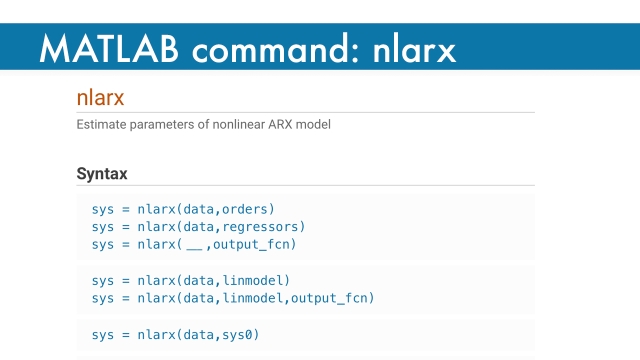
Check this out if you want a little more information into how the nlarx MATLAB command works.

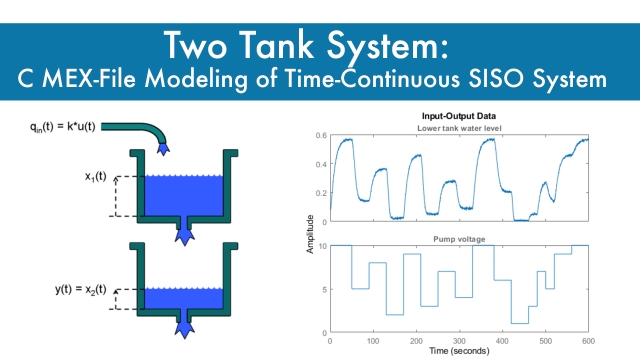
I didn't run this example in the video, but I used the first section where the system differential equations were derived using first principles.  By using this physical intuition, I was able to come up with a good nonlinear regressor that allowed for a better fit.

Nonlinear ARX models are just a subset of a larger class of polynomial models. This page does a great job explaining what they are and what each of the subset model structures are called.