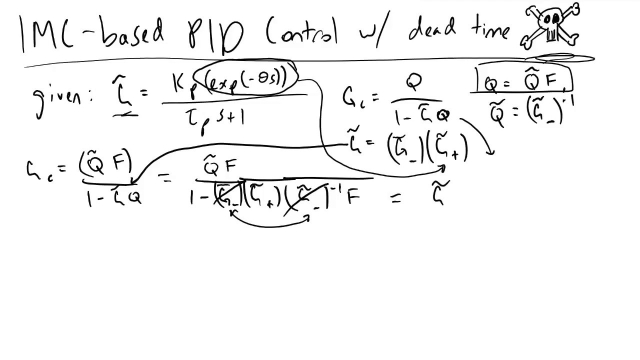
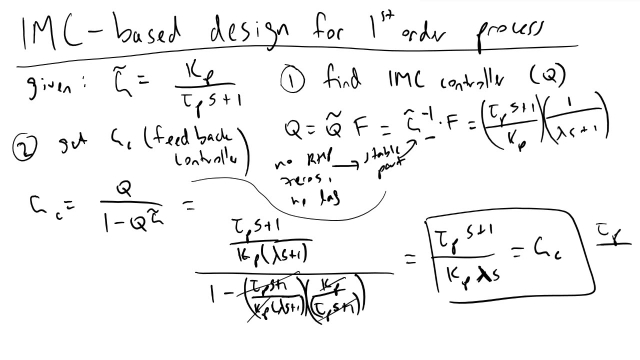
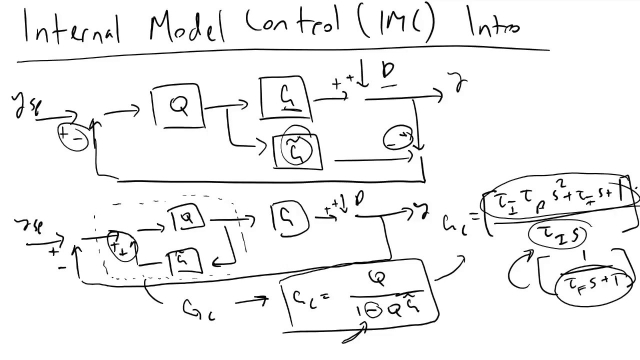
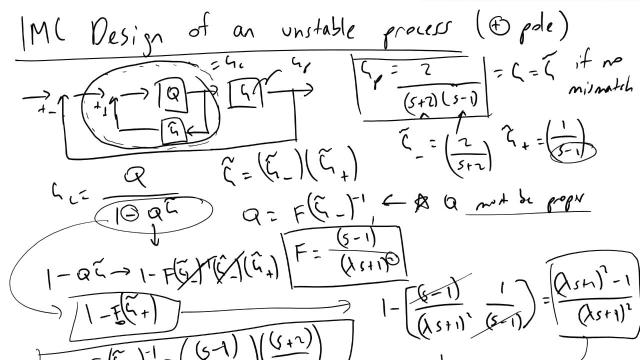
In the subject area of control theory, an internal model is a process that simulates the response of the system in order to estimate the outcome of a system disturbance. The internal model principle was first articulated in 1976 by B. A. Francis and W. M. Wonham as an explicit formulation of the Conant and Ashby good regulator theorem. It stands in contrast to classical control, in that the classical feedback loop fails to explicitly model the controlled system (although the classical controller may contain an implicit model).
The internal model theory of motor control argues that the motor system is controlled by the constant interactions of the “plant” and the “controller.” The plant is the body part being controlled, while the internal model itself is considered part of the controller. Information from the controller, such as information from the central nervous system (CNS), feedback information, and the efference copy, is sent to the plant which moves accordingly.
Internal models can be controlled through either feed-forward or feedback control. Feed-forward control computes its input into a system using only the current state and its model of the system. It does not use feedback, so it cannot correct for errors in its control. In feedback control, some of the output of the system can be fed back into the system’s input, and the system is then able to make adjustments or compensate for errors from its desired output. Two primary types of internal models have been proposed: forward models and inverse models. In simulations, models can be combined together to solve more complex movement tasks.