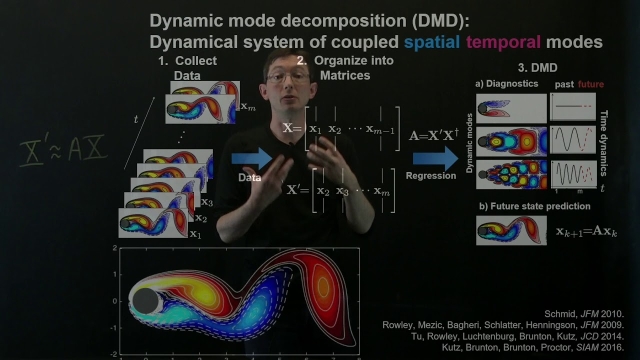
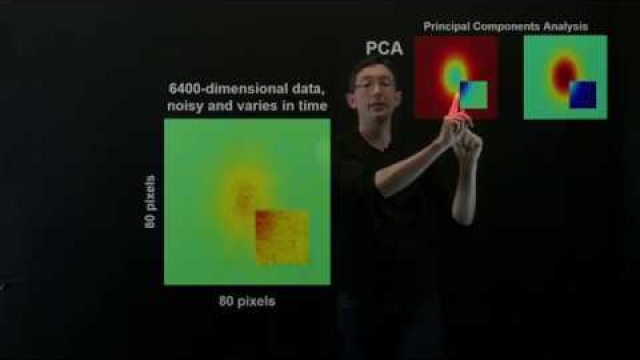
Dynamic mode decomposition (DMD) is a dimensionality reduction algorithm developed by Peter Schmid in 2008. Given a time series of data, DMD computes a set of modes each of which is associated with a fixed oscillation frequency and decay/growth rate. For linear systems in particular, these modes and frequencies are analogous to the normal modes of the system, but more generally, they are approximations of the modes and eigenvalues of the composition operator (also called the Koopman operator). Due to the intrinsic temporal behaviors associated with each mode, DMD differs from dimensionality reduction methods such as principal component analysis, which computes orthogonal modes that lack predetermined temporal behaviors. Because its modes are not orthogonal, DMD-based representations can be less parsimonious than those generated by PCA. However, they can also be more physically meaningful because each mode is associated with a damped (or driven) sinusoidal behavior in time.

from Dynamic Mode Decomposition - Wikipedia