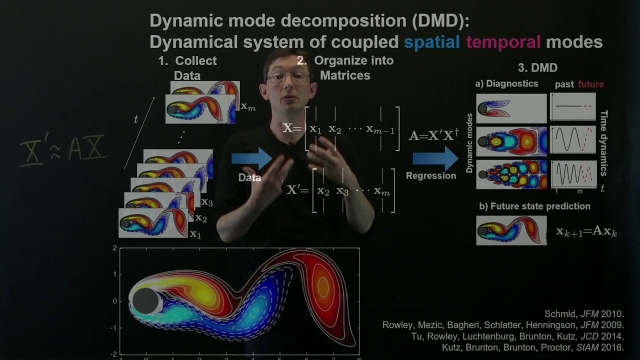
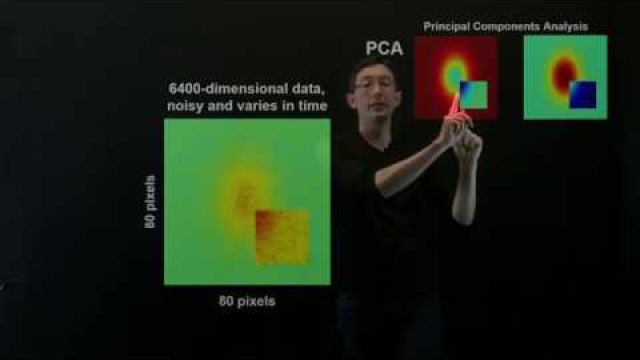
Dynamic mode decomposition (DMD) is a dimensionality reduction algorithm developed by Peter Schmid in 2008. Given a time series of data, DMD computes a set of modes each of which is associated with a fixed oscillation frequency and decay/growth rate. For linear systems in particular, these modes and frequencies are analogous to the normal modes of the system, but more generally, they are approximations of the modes and eigenvalues of the composition operator (also called the Koopman operator). Due to the intrinsic temporal behaviors associated with each mode, DMD differs from dimensionality reduction methods such as principal component analysis, which computes orthogonal modes that lack predetermined temporal behaviors. Because its modes are not orthogonal, DMD-based representations can be less parsimonious than those generated by PCA. However, they can also be more physically meaningful because each mode is associated with a damped (or driven) sinusoidal behavior in time.
Topic
Dynamic Mode Decomposition
This topic includes the following resources and journeys:
Filters
Type
Experience
Scope
3 items
Dynamic Mode Decomposition (Overview)
18 min
Intermediate
Video
Theory
In this video, we introduce the dynamic mode decomposition (DMD), a recent technique to extract spatio-temporal coherent structures directly from high-dimensional data. DMD has been widely...
See MoreDynamic Mode Decomposition (Examples)
7 min
Intermediate
Video
Theory
In this video, we continue to explore the dynamic mode decomposition (DMD). In particular, we look at recent methodological extensions and application areas in fluid dynamics, disease...
See MoreDynamic Mode Decomposition (Code)
8 min
Intermediate
Video
Application
In this video, we code up the dynamic mode decomposition (DMD) in Matlab and use it to analyze the fluid flow past a circular cylinder at low Reynolds number.
See More